Criterio de Routh–Hurwitz.
Este criterio es usado en sistemas de tiempo continuo para
determinar si el denominador de la función de transferencia tiene raíces en el semiplano
derecho del plano s. Si este criterio es aplicado a la ecuación
característica de un sistema de tiempo discreto expresado en la variable z,
no puede obtenerse ninguna información sobre la estabilidad del mismo. Sin
embargo, si la ecuación característica es expresada como una función de la
variable de transformación bilineal w, entonces la estabilidad
del sistema puede ser determinada por aplicación directa del criterio
de Routh–Hurwitz, de la misma manera que se aplica a los sistemas de
tiempo continuo. Esto es posible, pues a través de la transformación w el
interior del círculo unitario del plano z se transforma en el
semiplano izquierdo del plano w, y el exterior del círculo unitario
en el semiplano derecho w
En el análisis de estabilidad, utilizando la
transformación bilineal junto con el criterio de estabilidad
de Routh, primero se pondrá 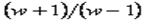
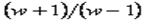
en lugar de z en la ecuación característica:
Entonces, si se simplifica las fracciones
multiplicando ambos miembros de esta última ecuación por se obtiene:
se obtiene:
 se obtiene:
se obtiene:
Una vez que se transforma  en
en  es posible aplicar el criterio de estabilidad
de Routh de la misma forma que en los sistemas en tiempo continuo.
es posible aplicar el criterio de estabilidad
de Routh de la misma forma que en los sistemas en tiempo continuo.
 en
en  es posible aplicar el criterio de estabilidad
de Routh de la misma forma que en los sistemas en tiempo continuo.
es posible aplicar el criterio de estabilidad
de Routh de la misma forma que en los sistemas en tiempo continuo.
ejemplo :
Para analizar la aplicación del criterio de estabilidad
de Routh–Hurwitz se utilizará el siguiente ejemplo:
El sistema de control de tiempo continuo, es estable para
todo valor positivo de la ganancia K. En efecto, si se aplica el
criterio de Routh–Hurwitz a su ecuación característica:
resultado :
El número de cambios de signo de la primera fila del arreglo
de Routh–Hurwitz indica el número de raíces del polinomio
característico P(s) ubicadas en el semiplano derecho. En
este caso no existen cambios de signo de modo que el sistema de tiempo continuo
realimentado en forma unitaria es estable para todo valor positivo de la
ganancia K
La función de transferencia entrada–salida para el
sistema equivalente de tiempo discreto, para un período de muestreo T =
0.1 s está dada por:
Para aplicar el criterio de Routh–Hurwitz es
necesario aplicar previamente la transformación bilineal:
Luego, la ecuación característica en el plano w está
dada por:
La aplicación del criterio
de Routh–Hurwitz conduce al siguiente arreglo:
Para que el sistema sea estable no debe haber cambios de
signos en la primera columna del arreglo, siendo necesario que la
ganancia K se halle comprendida en el rango:
Si se elige, en cambio, un período de muestreo mayor, por
ejemplo T = 1 s, se obtiene:
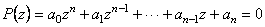












Excelente informacion
ResponderBorrarExcelente información, me sirvió para un trabajo de la escuela.
ResponderBorrarMuy buenas fuentes de información.